多くの複雑な現象は、短距離および長距離の力によって相互作用する点粒子の集合として記述することができる。このモデリング枠組みは、重力崩壊、半導体中の電子輸送、統計物理における運動論方程式など、古典的な多体問題の研究に端を発しており、近年では物理学の他分野に加え、生物学、社会科学、機械学習、さらには最適化分野にも応用が広がっている(Carrillo et al. 2010, 2019g, 2022c, 2018a; Bailo et al. 2024)。その結果、凝集–拡散モデルは現在、非常に活発な研究分野となっている。
これらのモデルは、微視的スケールから巨視的スケールまで幅広く適用可能であり、イオンチャネル輸送、化学走性、細菌の配向、細胞接着、血管新生、動物の群集行動、人間の群衆運動など、多様な応用を持つ。こうした系における個体間相互作用は、リガンド結合や電気的相互作用、社会的嗜好に由来する長距離の引力と、体積制約や混雑による短距離の斥力の組み合わせとして表現されることが多い。
セルオートマトンや駆動ブラウン粒子モデルなど、さまざまなエージェントベースの微視的手法が提案されているが、これらの振る舞いを厳密に理解するためには、粒子数が非常に大きくなった極限である平均場極限の解析が最も有効である(Oelschläger 1990a; Bolley et al. 2011; Jabin 2014)。
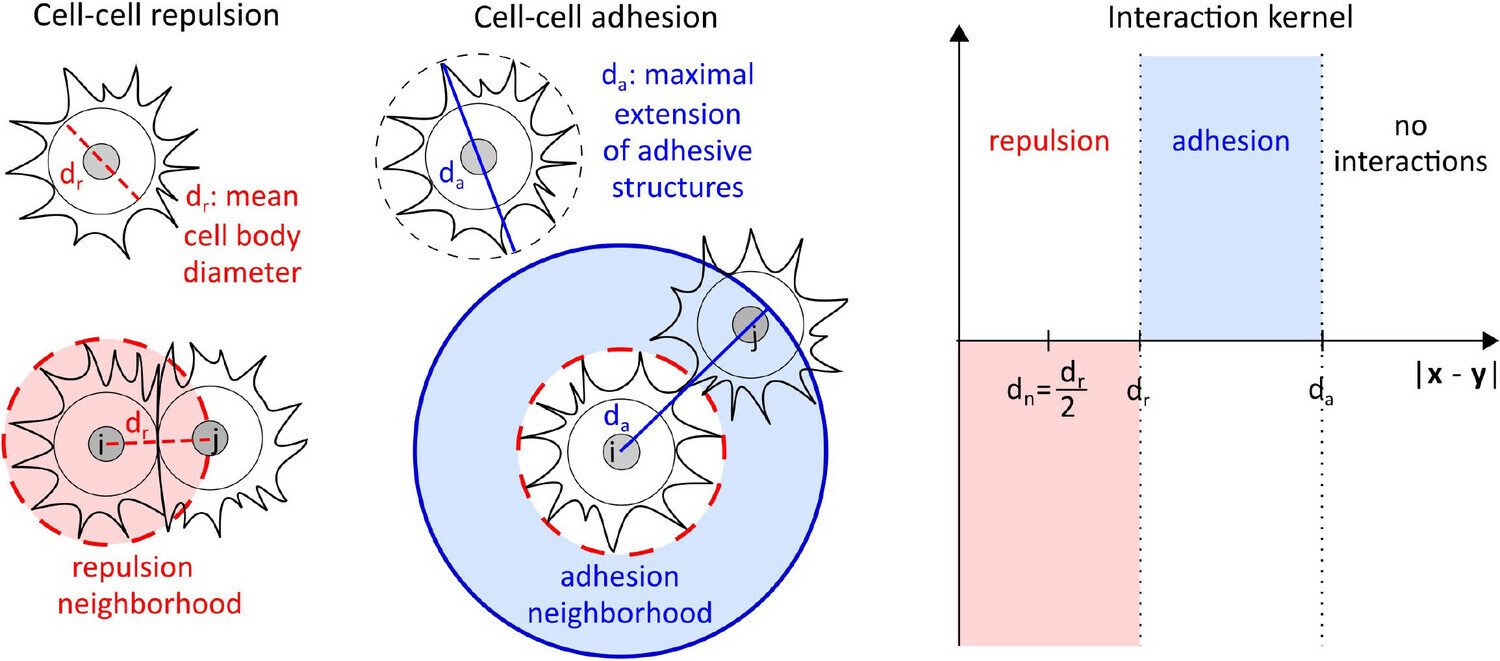
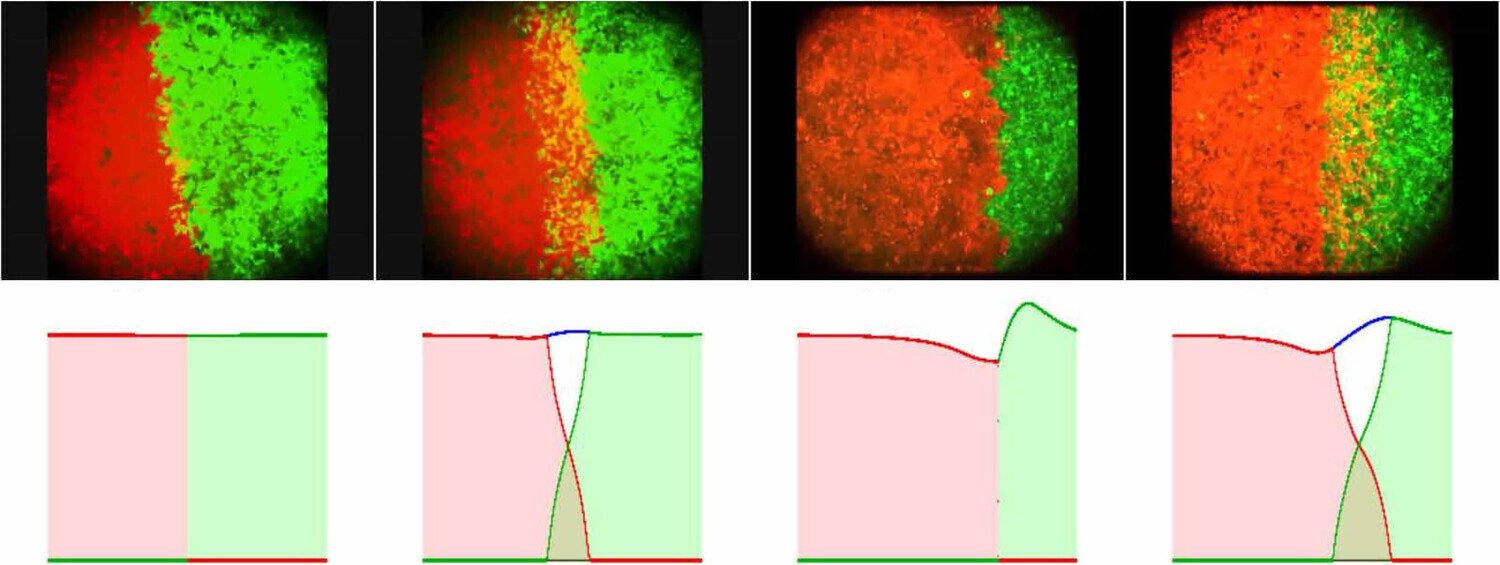
例として、異なる表面タンパク質やリガンド(カドヘリンやネクチンなど)を発現する2種類の細胞集団を考える。第1種の細胞核の位置を {xi}i=1N\{x_i\}_{i=1}^N{xi}i=1N、第2種を {yj}j=1M\{y_j\}_{j=1}^M{yj}j=1M とし、簡単のため N=MN = MN=M と仮定する。細胞は中距離での引力(フィロポディアを介した相互作用など)と、サイズや体積制約による短距離での強い斥力によって相互作用する。相互作用力が放射対称かつ保存力であると仮定すると、微視的モデルは粒子の運動方程式として定式化できる。
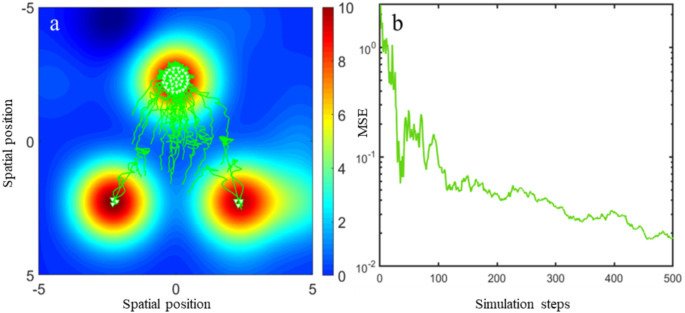
適切な条件の下で、このモデルに対応する経験測度は、多粒子極限において正規化された巨視的細胞密度へと収束する。生物学的文脈では、引力は有限のカットオフ半径内でのみ作用し、斥力は局所的であると考えるのが自然である(Calvez and Carrillo 2012)。この考えに基づき、相互作用ポテンシャルは N→∞N \to \inftyN→∞ の極限で WabN=εδ0+WabW^{N}_{ab} = \varepsilon \delta_0 + W_{ab}WabN=εδ0+Wab とスケーリングされる。
この極限により、平均場凝集–拡散モデルが得られる。より一般的には、集団密度 ρ(t,x)\rho(t,x)ρ(t,x) の時間発展は次の連続体方程式で表される:
∂tρ+∇⋅(ρu)=0,u=−∇ξ,ξ=U(ρ)+V+W∗ρ.\partial_t \rho + \nabla \cdot (\rho u) = 0, \quad u = -\nabla \xi, \quad \xi = U(\rho) + V + W * \rho.∂tρ+∇⋅(ρu)=0,u=−∇ξ,ξ=U(ρ)+V+W∗ρ.
ここで速度場は、拡散、外部ポテンシャルによるドリフト、そして対称な非局所相互作用のバランスによって決定される。
Citation:
TY - CHAP
AU - Bailo, Rafael
AU - Carrillo, J.A
AU - Gómez-Castro, David
PY - 2026/01/12
SP - 177
EP - 200
SN - 978-981-95-1445-8
T1 - Aggregation-Diffusion Equations for Collective Behaviour in the Sciences
VL -
DO - 10.1007/978-981-95-1446-5_9
ER -
For full paper:
https://www.researchgate.net/publication/399682810_Aggregation-Diffusion_Equations_for_Collective_Behaviour_in_the_Sciences